Howtosignalprocessing
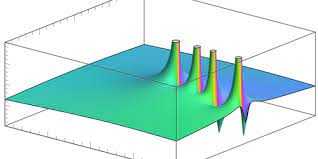
Fungsi Riemann Zeta, Fungsi Berguna dalam Teori Angka untuk Menyelidiki Sifat Bilangan Prima. Ditulis sebagai ζ (x), awalnya didefinisikan sebagai seri tak terbatas ζ (x) = 1 + 2-x + 3-x + 4-x + ⋯. Saat x = 1, seri ini disebut seri harmonik, yang meningkat tanpa terikat - saya.e., Jumlahnya tidak terbatas.
- Untuk apa fungsi Riemann Zeta digunakan?
- Bagaimana Anda menghitung fungsi Riemann Zeta?
- Siapa yang memecahkan fungsi Riemann Zeta?
- Apakah fungsi Riemann Zeta telah dipecahkan?
Untuk apa fungsi Riemann Zeta digunakan?
Fungsi Riemann Zeta mengkodekan informasi tentang bilangan prima-atom aritmatika dan kritis terhadap kriptografi modern di mana e-commerce dibangun. Menemukan Bukti adalah Cawan Suci Teori Angka Sejak Riemann pertama kali menerbitkan hipotesisnya.
Bagaimana Anda menghitung fungsi Riemann Zeta?
\ zeta (s) = \ sum_ n = 1^\ infty \ dfrac 1 n^s. ζ (s) = n = 1 ∞ ns1. Ini kemudian didefinisikan oleh kelanjutan analitik ke fungsi meromorfik pada keseluruhan C \ mathbb C C oleh persamaan fungsional.
Siapa yang memecahkan fungsi Riemann Zeta?
Nilai -nilai fungsi Riemann Zeta bahkan pada bilangan bulat positif dihitung oleh Euler. Yang pertama, ζ (2), memberikan solusi untuk masalah Basel. Pada tahun 1979 Roger Apéry membuktikan irasionalitas ζ (3).
Apakah fungsi Riemann Zeta telah dipecahkan?
Hipotesis Riemann, formula yang terkait dengan distribusi bilangan prima, tetap belum terpecahkan selama lebih dari seabad.
